Test de Razonamiento Deductivo con Figuras

Aunque utiliza figuras en vez de números, este test evalúa el pensamiento deductivo de abstracción numérica.

Las representaciones numéricas abstractas no simbólicas son importantes para evaluar el CI porque pueden proporcionar la base evolutiva y de desarrollo del pensamiento matemático¹.

Instrucciones

Este test utiliza ejercicios con cuadrados latinos para evaluar el razonamiento deductivo.

Los cuadrados latinos siguen dos reglas importantes:

1. Cada columna y línea deben contener un símbolo de cada tipo.

2. Cada columna y línea no pueden contener símbolos repetidos.

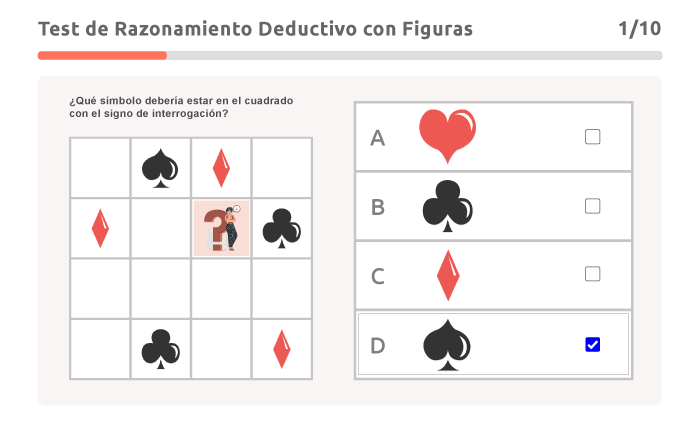
Para cada pregunta, se presentará un cuadrado latino de 4 x 4, parcialmente relleno. Una de las celdas tendrá un signo de interrogación.

Debes seleccionar de entre las respuestas la figura que debe reemplazar el signo de interrogación.

Ejemplo de test:

Descargo de responsabilidad:

Este test ha sido desarrollado con un propósito educacional y de entretenimiento. Los resultados no constituyen una evaluación psicológica o psiquiátrica de ningún tipo y pueden no ofrecer un retrato preciso de la aptitud mental del examinado. No garantizamos la exactitud de los resultados y los mismos no deben ser utilizados como un indicador de las capacidades del individuo para un propósito específico.

Las respuestas pueden ser registradas y utilizadas para fines de investigación o para distribuirse de otro modo. Todas las respuestas se registran de forma anónima.

¿Qué evalúan los test de razonamiento deductivo con figuras?

Un test de razonamiento deductivo evalúa la capacidad del examinado para usar sus habilidades de razonamiento deductivo. Esto se refiere a la capacidad de analizar declaraciones particulares para extraer conclusiones generales. Cuanta más información o declaraciones tenga una persona a su disposición, más precisas serán las conclusiones.

Los test de razonamiento deductivo con figuras añaden otro elemento a su valoración ya que las figuras también implican el uso del pensamiento abstracto. Para añadir otra dimensión a su análisis, la mayoría de estos test también emplean cuadrados latinos en sus preguntas. Estos cuadrados traen a la ecuación el razonamiento matemático, incluso cuando usan figuras abstractas no numéricas.

Las reglas que rigen los cuadrados latinos son simples: cada columna y línea debe contener un símbolo o número de cada tipo, sin repeticiones. El Sudoku, por ejemplo, es un rompecabezas de números basado en los cuadrados latinos

¿Cómo funcionan los test de razonamiento deductivo con figuras?

Las preguntas utilizadas en los test de razonamiento deductivo con figuras siguen los mismos principios que el Sudoku, pero con dificultades añadidas. Al igual que en el juego de rompecabezas, los examinados encontrarán un cuadrado latino parcialmente rellenado para cada pregunta. Sin embargo, en lugar de completar todos los espacios en blanco, se les pedirá que señalen el símbolo o número que se debe colocar en una celda específica.

Esto los obliga a resolver la pregunta a mano, estructurando sus pensamientos y razonamiento mediante el uso de una ayuda visual, o a emplear su memoria en un grado superior. De cualquier manera, los examinados tendrán que usar el pensamiento abstracto y el razonamiento deductivo para encontrar la respuesta. Por ejemplo, dependiendo de la ubicación de las celdas ya ocupadas, es posible que tengan que hacer suposiciones para completar la pregunta, probarlas y descartarlas cuando se demuestre que son falsas.

Acerca de los cuadrados latinos

Los cuadrados latinos fueron desarrollados por primera vez por Leonhard Euler en 1776, como un sistema matemático para ser utilizado en análisis estadísticos. El matemático y físico suizo combinó los conceptos de Cuadrado Latino, una matriz rellenada con letras del alfabeto latino, con el de Cuadrados Mágicos que se rellenan de números siguiendo una fórmula matemática que asegura que la suma de cada línea y columna sea siempre la misma.

En su artículo titulado “De quadratis magicis”, Euler usó tablas de 3x3, 4x4, 5x5 y 6x6 para demostrar que, cuando se aplican ciertas restricciones, los principios y conceptos de un Cuadrado Mágico también se pueden lograr usando el alfabeto latino.

Hoy en día, el concepto de Euler del cuadrado latino va más allá del alfabeto latino. Ahora se sabe que cuando existe la restricción de llenar cada línea y columna con un elemento de un tipo sin repeticiones, el principio de los cuadrados latinos se puede replicar utilizando cualquier tipo de símbolo.

Referencias:  

¹ Cantlon, J., Cordes, S., Libertus, M. & Brannon, E. (2002). Numerical abstraction: It ain’t broke. Behavioral and Brain Sciences. 23 (3/4), 331-332.