Test de Series Numéricas

Presentar una secuencia numérica y preguntar cuál podría ser el siguiente número es una de las pruebas más comunes en la evaluación de la inteligencia porque traduce la capacidad de uno para detectar una regla no especificada de un conjunto de datos, algo que está altamente asociado con el aprendizaje¹ y el potencial de aprendizaje².

El razonamiento inductivo puede ser útil en muchas situaciones de resolución de problemas y es comúnmente utilizado por los profesionales de las matemáticas³.

Instrucciones

Para cada pregunta se presentará una serie numérica distinta. Debes seleccionar el número que completa cada secuencia y que debe reemplazar el signo de interrogación.

Ejemplo: 2 - 4 - 6 - 8 - ?

La secuencia sigue una estructura de 2 + 2 + 2 + 2, por lo tanto, el número que completa las secuencias es el 10. Todos los números son múltiplos de 2.

Ejemplo de test:

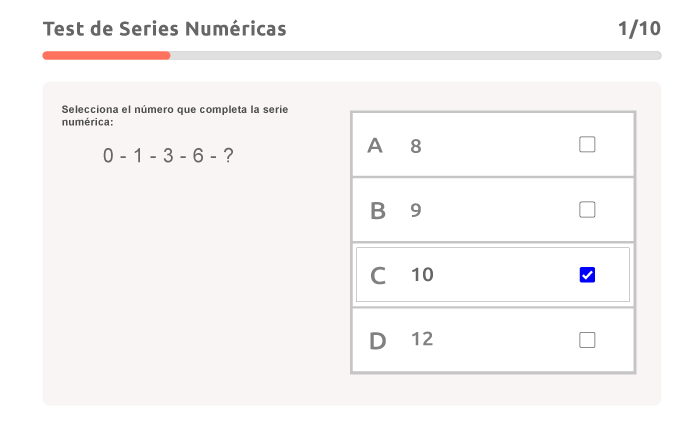
Descargo de responsabilidad:

Este Test de Series Numéricas ha sido desarrollado con un propósito educacional y de entretenimiento. Los resultados no constituyen una evaluación psicológica o psiquiátrica de ningún tipo y pueden no ofrecer un retrato preciso de la aptitud mental del examinado. No garantizamos la exactitud de los resultados y los mismos no deben ser utilizados como un indicador de las capacidades del individuo para un propósito específico.

Las respuestas pueden ser registradas y utilizadas para fines de investigación o para distribuirse de otro modo. Todas las respuestas se registran de forma anónima.

Serie de números - patrones comunes

Serie monótona

Las series monótonas se crean únicamente a través de la adicción y sustracción, por lo que sus patrones son de los más fáciles de identificar en cualquier test de razonamiento numérico.

No obstante, existen variaciones de las series básicas que pueden dificultar la identificación de la regla que las rige. Estas variaciones generalmente se basan en patrones que no se perciben inmediatamente a primera vista.

Un ejemplo de una serie monótona sencilla podría ser 1 - 2 - 3 - 4. Aquí el patrón sería sumar +1 a cada número para formar la secuencia. 

En el caso de una más compleja, podría pasar que el tercer número se obtiene sumando la diferencia entre el primero y el segundo. 

Por ejemplo: 0 - 2 - 6 - 12 - 20

En este caso, se suma +2 a la diferencia entre los números en la secuencia para encontrar el siguiente:

0 - 2 (+2 +2) 6 (+2 +4) 12 (+2 +6) 20

Serie exponencial

Las series exponenciales se pueden lograr a través de la multiplicación y la división, aunque también pueden incluir sumas y restas para crear series y patrones más complejos.

En series simples, los números siempre se multiplican o dividen por el mismo dígito. Tomemos como ejemplo la serie 2 - 4 - 16 - 128. El salto del 4 al 16 y luego al 128 ya insinúa que lo más probable es que no se trate de una serie monótona. Una mirada más cercana puede decirte que cada número se multiplica por sí mismo para encontrar el siguiente:

2 x 2 = 4
4 x 4 = 16
16 x 16 = 128

En los más complejos, el número responsable de la multiplicación puede cambiar siguiendo un patrón de suma o resta.

Por ejemplo, en la secuencia 2 - 4 - 12 - 48, la serie exponencial se ve afectada por la adición de +1 a la multiplicación en cada paso:

2 x 2 = 4
3 x 4 = 16
4 x 16 = 48

Por lo tanto, el siguiente número de esta serie sería 240 (5 x 48).

Un buen consejo para recordar en el caso de series exponenciales es tratar de dividir cada número por el anterior para verificar si son múltiplos y si hay un patrón allí.

Patrón alterno

En este tipo de series, el patrón no es inmediatamente obvio. Normalmente, los números pueden aumentar o disminuir en las secuencias, con saltos que en un principio no parecen lógicos.

Como su nombre indica, este tipo de series esconden un patrón alterno que puede contener sumas, restas, multiplicaciones y divisiones, aisladas o combinadas. Un ejemplo de un patrón alternante simple sería: 1 - 3 - 6 - 8 - 11. El patrón aquí alterna entre sumar +2 y +3 al número anterior:

1 + 2 = 3
3 + 3 = 6
6 + 2 = 8
8 + 3 = 11

Los patrones más complejos pueden ser más largos. Un buen consejo es verificar siempre si hay una multiplicación o suma cuando el número aumenta y si hay una resta o división cuando disminuye.

Patrones entrelazados

Las secuencias entrelazadas contienen dos o más patrones independientes entre sí. En este tipo de series, no hay relación entre los números que se suceden directamente.

En secuencias simples entrelazadas, los patrones tienden a saltar entre posiciones pares e impares. Tomemos la siguiente secuencia como ejemplo: 2 - 0 - 4 - 4 - 6 - 8. Aquí las posiciones impares aumentan en +2 mientras que las posiciones pares aumentan en +4.

Cuanto más largas son las secuencias, más patrones contienen, y cuanto más largos son los saltos entre los patrones, más difícil es detectar las reglas que las gobiernan.

Fibonacci

Los test de series de números tienden a incluir al menos una secuencia de Fibonacci para confundir a los examinados. En estas secuencias cada número es siempre la suma de los dos anteriores. En ejercicios sencillos, la secuencia tiende a comenzar con el cero para que sea más fácil detectar el patrón. En los más difíciles, la secuencia puede comenzar con cualquier número.

Sin embargo, también existen ejercicios basados en la lógica de Fibonacci, pero con variaciones. Por ejemplo, cada número puede ser el resultado de restar, multiplicar o dividir los dos anteriores. En el caso de las restas y divisiones también importa de qué número se va a dividir o restar.

Fracciones

Hay dos tipos de series numéricas que contienen solo fracciones. El que es más común en los test de CI tienden a seguir una de las lógicas mencionadas anteriormente. Es decir, siguen los mismos patrones que los números enteros, pero se presentan en la forma de fracciones.

El otro tipo es más complicado porque puede contener diferentes patrones en el numerador y denominador al mismo tiempo o solo en uno de ellos.

Referencias:

¹ Angluin D., Smith C.H. (1983). Inductive inference: Theory and methods. Comput. Surveys, 15 (1983), pp. 237-269.

² Csapó, B. (1997). The Development of Inductive Reasoning: Crosssectional Assessments in an Educational Context. International journal of behavioral development. 20 (4), 609–626.

³ Pólya, G. (1954). Induction and Analogy in Mathematics. Princeton University Press. p. 120.